maturité ET CONTROVERSES







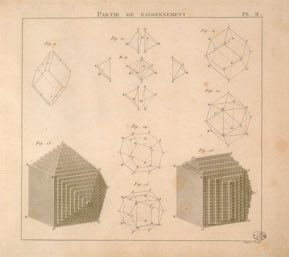
Avec son modèle de structure, Haüy peut prévoir toutes les formes possibles. Pour ce faire, il faut une forme primitive, un cube par exemple, sur lequel on empile des couches décroissantes de molécules intégrantes.
L’APPort mathématique d’Haüy
En plus d'être botaniste et ecclésiastique, Haüy avait la « bosse des maths ». Mais pas au point d’être mathématicien notamment en 3 dimensions, ce dont la maîtrise lui fit défaut.
Cependant, Haüy repère immédiatement une faille du « dodécaèdre à plans triangulaires » chez Romé (trop complexe) et la corrige dans ses définitions énoncées en 1784 : il le remplace par le « prisme hexaèdre » (comprendre le prisme hexagonal) plus simple et donc plus « efficace ».
dodécaèdre
à plans triangulaires de Romé


prisme
hexaèdre d’Haüy
« Homme de Vitruve » de Leonard de Vinci ©wikimedia
-
-la première condition est que ces décroissements soient simples,
-
-la seconde stipule que si on commence un empilement sur une face, ici du cube, il est également transposé sur toutes les autres faces similaires à la première.
MAUDITE TOURMALINE, MAUDITE COBALTITE, MAUDITE PYRITE...
Mais certains cristaux — ces « merveilleuses exceptions » (Haüy réfère ici aux mériédries)— ne suivent pas cette loi.
Haüy réplique que des impuretés ou autres défauts en sont la cause...
En bref, la maturité devient compliquée... comme souvent (et ici aussi...).
la loi des décroissements rationnels
Dans cet opus (1809), Haüy reconnait les remarques - pour ne pas dire les critiques - du chimiste Claude Louis Berthollet (1748-1822) concernant certaines incohérences entre composition chimique et molécule intégrante proposée par clivage.
LE Tableau comparatif de 1809
Haüy reprend ses travaux et cherche à montrer alors qu’une molécule intégrante spécifique est caractérisée par une composition chimique particulière parmi plusieures possibles quand, dans un cristal donné, plusieurs compositions peuvent être présentes.
Pour Haüy, ces variations contrôlent probablement les formes extérieures des minéraux. Des « accidents » selon Haüy - comprendre des modifications impliquant des variétés d’espèce - influencent divers facteurs comme la composition chimique, les habitus cristallins, la densité, la dureté, les propriétés optiques quand bien même la géométrie de la molécule intégrante reste constante.
Dans son Traité de Cristallographie (1822) Haüy ira même à « prouver » que la cristallographie est la science la plus fidèle à la nature des minéraux car la chimie, en détruisant le minéral pour l’analyse, en donne une vision déformée. L’analyse chimique est qualifiée d’ « opération dont les résultats ont effacé leurs traits caractéristiques » (Haüy, Traité de cristallographie, 1822, tome I, Introduction, p. I).

Haüy impose alors deux conditions à ces empilements, c’est sa « loi de symétrie » :
Haüy réfute, puis justifie puis tente d’innover pour « sauver sa théorie » comme le dit Bernard Maitte (2001) en proposant diverses « justifications » des plus complexes : les lois des décroissements rationnels (1811) puis celle dite « de symétrie » (1815).
Ces controverses sont complexes et Haüy d’autant que le style d’écriture d’Haüy est lourd et complexe à suivre : Bernard Maitte (2001) en décode les principes avec bravoure (cette lecture reste, cependant, ardue à suivre).

Mais d’autres controverses apparaissent, notamment les différences d’angles de clivage de la calcite entre celles mesurées par Haüy et celles du physico-chimiste brittanique William Hyde Wollaston (1766-1828). Ce dernier utilise un goniomètre optique bien plus précis qui montre que les rapports « simples » de la théorie d’Haüy ne sont pas si justes.
Goniomètre de Wollaston : Tiens, un anglais !
Cet instrument (1809) utilise la réflexion de la lumière à la mesure des angles que font entre elles les facettes d’un cristal. Pour mesurer un tel angle, on mesure successivement la direction de la lumière réfléchie par chacune des deux facettes, ce qui permet de déterminer l’angle entre ces deux dernières. Si ce procédé est l’invention du physicien parisien Etienne-Louis Malus (1775-1812), c'est Wollaston qui l'a rendu célèbre en cristallographie : cet instrument simple et portable donne une mesure plus précise que le « mesure-angle » de Carangeot. De plus, ce goniomètre optique est particulièrement adapté à la mesure de petits cristaux aux facettes brillantes.

un goniomètre de Wollaston
©wikimedia

William Hyde Wollaston
©wikimedia
L’abbé est poussé dans ses retranchements. Il est persuadé avoir raison puisque qu’il affirme « On reconnaît ici ce qui caractérise en général les lois émanées de la puissance et de la sagesse du Dieu qui l'a créée et qui la dirige. Economie et simplicité dans les moyens, richesse et fécondité inépuisable dans les résultats ».
Avec d’autres mots, le contrarier serait presqu’hérésie contre Dieu.

la loi de symétrie (1815)


L’école allemande de la cristallographie,
Christian Samuel Weiss en premier,
va résoudre ces exceptions avec une autre théorie,
basée sur les axes de symétrie,
d’où jaillieront les systèmes cristallins.
Cependant, cette école allemande rejeta
l’approche moléculaire (« atomistique ») française
pour une autre, focalisée autour d’ondes et d’énergies.
Ainsi, la voie allait être ouverte pour une unification des deux concepts, moléculaire et symétries : ce sera l’honneur de Gabriel Delafosse, le dernier étudiant d’Haüy.
De surcroît, dans un soucis constant de simplification rationnelle qui doit avoir un lien culturel avec sa profonde foi catholique (« proportion divine »), Haüy trouve qu’il est possible de décrire ces « formes primitives » avec seulement 3 de ses « molécules intégrantes » : le tétraèdre irrégulier, le prisme triangulaire et le cube.


Avec la vieillesse, les soucis s’accumulent : si les douleurs aigües finissent par s’oublier, les joutes scientifiques redoublent : le maître vacille.