maturitY and CONTROVERSIES



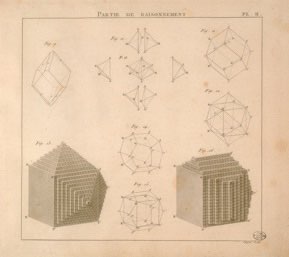
With his model of structure, Haüy can predict « all » (most?) possible shapes. To do this, one needs a primitive shape, a cube for example, on which one stacks decreasing layers of integral molecules.
THE mathEmatICAL OF Haüy
In addition to being a botanist and an ecclesiastic, Haüy was also a "math whiz". But not to the point of being a mathematician, especially in 3 dimensions that will be source of troubles.
However, Haüy immediately spotted the flaw in Romé's "dodecahedron with triangular planes" (too complex shape) and corrected it in his definitions in 1784: he replaced it with the "hexahedron prism" (to understand the hexagonal prism), which was a simpler shape and, therefore, more "efficient" for his theories.
dodécaèdre
à plans triangulaires de Romé
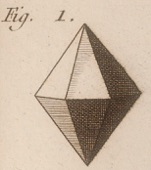

prisme
hexaèdre d’Haüy
« Vitruvus man » of Leonardo da Vinci ©wikimedia
-
-the first condition is that these decreases are simple
-
-the second stipulates that if we start a stacking on a face, here of the cube, it is also transposed on all the other faces similar to the first.
DAMNED TOURMALINE, DAMNED COBALTITE, DAMNED PYRITE...
But some crystals - these "marvelous exceptions" by Haüy (he refers here more specifically to merohedry) - do not follow this law. Haüy replies that impurities or other defects are the cause...
In short, maturity becomes complicated... as it often does (as I am learning too).
THE LAW OF RATIONAL DECREMENTS (« décroissements rationnels»)
In this opus (1809), Haüy acknowledges remarks - if not criticisms - from French chemist Claude Louis Berthollet (1748-1822) concerning certain inconsistencies between chemical composition and integral molecule proposed by cleavage.
THE « Tableau comparatif... » OF 1809
Haüy resumed his work and tried to show that a specific integral molecule is characterized by a particular chemical composition among several possible ones when, in a given crystal, several compositions can be present.
For Haüy, these variations probably control the external shapes of minerals. The so-called "accidents" - to understand modifications involving varieties of species - are supposed to influence various factors such as chemical composition, crystal habit, density, hardness, optical properties even though the geometry of the integral molecule remains constant.
In his Treatise on Crystallography (1822) Haüy even goes so far as to "prove" that crystallography is the most faithful science to the nature of minerals because chemistry, by destroying the mineral for analysis, gives a distorted vision. The chemical analysis is qualified of "operation whose results erased their characteristic features" (volume I, Introduction, p. I).

Haüy then imposes two conditions on these decrements, his "law of symmetry":
Haüy refutes, then justifies, then tries to innovate to « save his theory » as Bernard Maitte (2001) wrote, by proposing various "justifications" of the most complex: the law of rational decrements (1811) and that of « of symmetry » (1815).
These controversies are complex and Haüy's writing style is heavy and complex to follow: Bernard Maitte (2001) deciphers (in French) these principles, not without bravery (still, this reading is alas! uneasy to comprehend).

But other controversies appear, in particular the differences of angles of cleavage of the calcite between those measured by Haüy and those of the British physicochemist William Hyde Wollaston (1766-1828). The latter used a much more precise optical goniometer which showed that the "simple" ratios of Haüy's theory were not so accurate.
THE Wollaston GONIOMETER: BRITS IN?
This instrument (1809) uses the reflection of light to measure the angles between the facets of a crystal. To measure such an angle, one measures successively the direction of the light reflected by each of the two facets, which makes it possible to determine their dihedral angle. If this process is the invention of the Parisian physicist Etienne-Louis Malus (1775-1812), it is William Hyde Wollaston who made it famous in crystallography: this simple and portable instrument gives a more accurate measurement than the "angle-measuring" of Carangeot. Moreover, this optical goniometer is particularly adapted to the measurement of small crystals with brilliant facets..

A Wollaston goniometer
©wikimedia

William Hyde Wollaston
©wikimedia
The abbot is pushed into a corner. He is convinced that he is right, since he states: "One recognizes here what characterizes in general the laws emanating from the power and wisdom of the God who created it and who directs it. Economy and simplicity in the means, richness and inexhaustible fruitfulness in the results".
In other words, to contradict him would be almost heresy against God.

la "loi de symétrie" (1815)
The German school, Christian Samuel Weiss first, will solve those exceptions with another theory, based on symmetry axes, hence the crystal systems.
However, this German school will reject the molecular approach for another one dealing with energies and waves.
Therefore the path will be open for an unification of both concepts, molecular and symetries : this will be Gabriel Delafosse’s work, the last student of Haüy.




Moreover, in a constant concern of rational simplification which must have a cultural link with his deep catholic faith ("divine proportion"), Haüy finds that it is possible to describe these "primitive forms" with only 3 of its "integral molecules": the irregular tetrahedron, the triangular prism and the cube.


With old age, the worries accumulate: if the acute pains end up being forgotten, the scientific jousts redouble: the master falters.